10329. Игра с камушками

Чтобы скоротать время, корова Бесси и ее подруга Элси любят играть в аналог игры, которую они видели на окружной ярмарке.

Для начала Бесси кладет три перевернутые ракушки на стол и кладет под одну из них небольшой круглый камешек (по крайней мере, она думает что это камешек, так как нашла его на земле на одном из пастбищ). Затем Бесси меняет пары ракушек, а Элси пытается угадать местонахождение камешка.

Стандартная версия игры, которую видели коровы на ярмарке графства, позволяла игроку видеть начальное местоположение камешка, а затем требовалось угадать его окончательное местоположение после завершения всех обменов.

Однако коровы любят играть в версию, в которой Элси не знает начального местоположения камешка и где она может угадывать местоположение камешка после каждого обмена. Бесси, зная правильный ответ, в конце ставит Элси оценку, равную количеству правильных предположений, которые она сделала.

Учитывая обмены и предположения, но не исходное местоположение камешка, определите максимальный балл, который могла заработать Элси.

Вход. Первая строка содержит целое число n (1 ≤ n ≤ 100) – количество обменов. Каждая из следующих n строк описывает шаг игры и содержит три целых числа a, b и g, указывающих, что ракушки a и b были переставлены Бесси, после чего Элси предположила что камень находится под ракушкой g. Среди трех целых чисел встречаются только 1, 2 или 3. Известно, что a ≠ b.

Выход. Выведите максимальное количество очков, которое могла бы заработать Элси.

Пример. В приведенном примере Элси может заработать не более 2 очков. Если камешек изначально находился под ракушкой 1, то она угадала бы ровно один раз (в последнем предположении). Если камешек изначально был под ракушкой 2, то она угадает дважды (в первых двух попытках). Если камешек изначально был под ракушкой 3, то она не делает правильных предположений.

Пример входа

Пример выхода

1 2 1

3 2 1

1 3 1

РЕШЕНИЕ

моделирование

Анализ алгоритма

Камень может изначально находиться под первой, второй или третьей ракушкой. Рассмотрим каждый из этих трех случаев и для каждого из них вычислим количество очков, которое заработает Элси. Максимальное из них и будет ответом. Задача сводится к моделированию игры.

Пример

Промоделируем игру для трех случаев: когда камешек сначала находится под первой, второй и третьей ракушкой. Стрелками указаны предположения Элси.

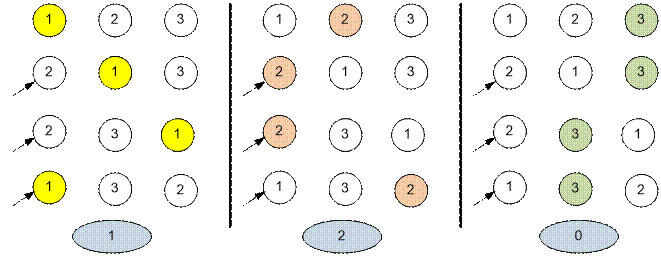
В первом случае Элси угадает 1 раз, во втором – два раза, в третьем – 0 раз. Максимальное количество очков, которое может заработать Элси, равно 2. Это будет в случае, когда камешек изначально находится под ракушкой номер 2.

Реализация алгоритма

Игра содержит не более 100 шагов, сохраняем их в массивах a, b и g.

int a[100], b[100], g[100];

Функция num_correct возвращает количество очков, которое получит Элси при условии что камешек изначально находится под ракушкой номер starting_shell.

int num_correct(int starting_shell)

{

Переменная current_shell содержит номер ракушки, под которой перед каждой итерацией находится камешек. Изначально current_shell = starting_shell.

int current_shell = starting_shell, correct = 0;

for (int i = 0; i < n; i++)

{

Если камешек находится в позиции a_i, то его следует переместить в позицию b_i (и наоборот).

if (a[i] == current_shell) current_shell = b[i];

else if (b[i] == current_shell) current_shell = a[i];

Если после обмена камешек находтся в позиции g_i, то Элси угадывает его положение и зарабатывает одно очко.

if (current_shell == g[i]) correct++;

}

return correct;

}

Основная часть программы. Читаем входные данные.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%d %d %d", &a[i], &b[i], &g[i]);

Перебираем все возможные начальные положения камня: i = 1, 2, 3. Для каждого из них вычисляем количество очков Элси. В переменной best находим максимум среди них.

int best = 0;

for (i = 1; i <= 3; i++)

best = max(best, num_correct(i));

Выводим ответ.

printf("%d\n", best);

Реализация алгоритма – моделирование

Шаги игры сохраняем в массивах a, b и g.

int a[100], b[100], g[100];

Читаем входные данные.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%d %d %d", &a[i], &b[i], &g[i]);

В переменной best вычисляем максимальный балл, который могла заработать Элси.

int best = 0;

Перебираем все возможные начальные положения камня: i = 1, 2, 3.

for (i = 1; i <= 3; i++)

{

Начальное положение игры кодируем в массиве m. Изначально камень лежит под ракушкой i: установим m[i] = 1, остальные ячейки массива m обнулим.

int m[] = { 0, 0, 0, 0 };

m[i] = 1;

В переменной cnt вычисляем количество правильных предположений Элси.

cnt = 0;

В массиве m моделируем n шагов игры. Меняем местами ракушки номер a[j] и b[j]. Если m[g[j]] = 1, то предположение Элси верно.

for (j = 0; j < n; j++)

{

swap(m[a[j]], m[b[j]]);

cnt += m[g[j]];

}

Находим максимум среди всех значений cnt.

if (cnt > best) best = cnt;

}

Выводим ответ.

printf("%d\n", best);

Python реализация – моделирование

Читаем количество обменов n.

n = int(input())

Шаги игры сохраняем в массивах a, b и g.

a = [0] * n

b = [0] * n

g = [0] * n

Читаем данные игры.

for i in range(n):

a[i], b[i], g[i] = map(int, input().split())

В переменной best вычисляем максимальный балл, который могла заработать Элси.

best = 0

Перебираем все возможные начальные положения камня: i = 1, 2, 3.

for i in range(1, 4):

m = [0, 0, 0, 0]

m[i] = 1

В переменной cnt вычисляем количество правильных предположений Элси.

cnt = 0

for j in range(n):

m[a[j]], m[b[j]] = m[b[j]], m[a[j]]

cnt += m[g[j]]

Находим максимум среди всех значений cnt.

if cnt > best:

best = cnt

Выводим ответ.

print(best)